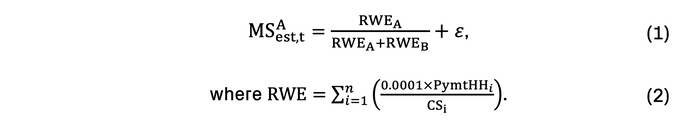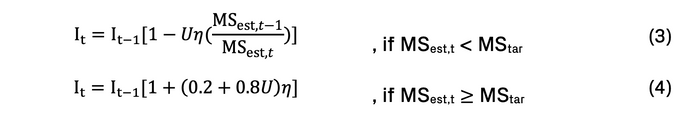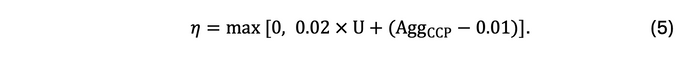Credit Card Model

Agent-based models (ABM) are commonly used to understand various scenarios in which the combination of actions taken by individual agents/entities may influence the overall dynamics of a system. It solves problems from the ‘bottom up’ rather than through rules imposed from the ‘top down’ and is becoming increasingly popular in the field of finance.

This documentation provides a description on a novel credit card model, which simulates the interactions between credit card providers and individual households. This is a simplified model provided as a proof-of concept.

Download Model Files

The credit card providers can adopt different sets of policies, in terms of interest rates and reward systems, to compete for market share by providing incentives for households to use their credit cards. An agent-based approach is particularly advantageous for this application and demonstrates many use cases. For example, it:

• Enable stakeholders to evaluate the non-linear effect of competition between credit card providers and demonstrates how the system gets to an equilibrium;

• Provides a tool for credit card providers to evaluate the short- and long- term impacts caused by policy changes from themselves or their rivals;

• Allow credit card providers to devise different strategies to achieve their targeted market share.

Agents & Network

There are two groups of agents in this model: (i) two credit card providers; and (ii) N number of households. Each household is linked with the two credit card providers. The network structure is shown in the figure below.

Each household are provided with two credit cards from Providers A and B. Currently, it is assumed that the credit limit for both credit cards are the same, and this is estimated according to their respective credit scores.

The household consumption consists of a subsistence and discretionary component, and the credit card providers essentially compete with each other to increase their market share by transaction volume. They do so by changing their interest rates and/or making the use of their credit cards more attractive by having a Reward Program.

The action taken by a credit card provider is expected to have a knock-on effect in the spending pattern of individual households. Additionally, the strategic interaction between credit card providers and households are modelled by game theory, where credit card providers may subsequently be forced to adapt its policies to remain competitive.

Input Parameters

The ABM requires two sets of input parameters to be specified, including the characteristics of individual households and competing credit card providers.

Credit Card Providers

1. Initial interest rate (I₀)

2. Reward factor (RF₁, RF₂)

3. Aggressiveness of credit card providers (Agg_CCP,1, Agg_CCP,2)

   • Adaptive (learning) rate to changing market conditions.

4. Market share target (MS_tar)

5. Market share estimate (MS_est)

6. Update frequency:

-	How often the banks can update their interest rates

Households

1. Number of households (N)

2. Income volatility

3. Aggressiveness of household (Agg_HH)

-	Adaption (learning) rate to changing terms (interest rates and reward factors) that are provided by credit card providers.

4. Average credit card usage

5. Average and minimum credit card repayment

6. Credit score (CS_i)

7. Credit limit (CL_i)

Model Overview

Once again, this is a simplified model provided as a proof-of concept.

Initialization

The model is initialized with N number of households with: (i) a starting wealth of $1000; (ii) an income that is sampled from an empirical distribution; (iii) a stochastic credit score that has values of between 0 and 1000; and (iv) a credit limit that is dependent on their respective credit score.

Individual households are also initialized with a 50:50 split in payments between their credit cards. Therefore, the two credit card providers have an initial market share of 50% respectively. The initial interest rate and reward factor for the two credit card providers is specified by the user.

Structure & Logic

At each time step, a small amount of income volatility for individual households (± 2.5% of the absolute income) is incorporated. We then use the Bank of England’s Consumption Model to simulate the subsistence and discretionary spending of each household: a constant amount of subsistence consumption is subtracted from the household wealth, while a portion of the discretionary consumption is paid with the two credit cards.

The households can pay this outstanding credit card payment either: (i) in full (when their wealth levels exceed the outstanding balance) — transactors; or (ii) in portion — revolvers. For scenario (ii), this portion is estimated based on their credit scores with a small random variation, and we currently assume that households with a higher credit score will pay a larger proportion of the outstanding balance.

In essence, the two credit card providers are trying to incentivize the households to increase spending using their respective cards via lower interest rates and providing a generous rewards system. The proportion of outstanding balance that is split between the two credit cards is determined by individual households with a utility function that takes into account both the interest rate and reward system from each credit card provider.

The credit card providers estimate their current market share (MS_est,t) after each step based on the proportion of its risk weighted exposure (RWE),

𝜀 is a random noise that is introduced to reflect incomplete information when estimating the market share. Eq. (2) weighs the payments made by each household (PymtHH_i) according to their credit score (CS_i), where the RWE is scaled upwards for households with a lower credit score.

Over time, the credit card providers can adaptively set its interest rate using a simplified version of the Delta Learning method (Widrow-Hoff Rule). The interest rate (I_t) is adapted according to the MS_est,t relative to its target market share (MS_tar),

where U is a random number with a standard uniform distribution, and 𝜂 is the learning rate that is calculated as follows,

The credit card provider is expected to reduce its interest rates if its current market share is below the targeted share (Eq. 3): interest rates reductions are larger in each time step when the credit card provider is losing market share (MS_est,t) relative to its previous time step (MS_est,t-1); and at smaller increments when it is gaining market share but still below its targeted market share. Conversely, a credit card provider can increase its interest rates to boost profits if the targeted market share has been achieved (Eq. 4). The learning rate (𝜂) from Eq. (5) dictates the aggressiveness of the credit card providers, i.e. their rate of change in their interest rates at each time step.

As the credit card providers alter their interest rates and rewards systems, individual households will also respond to these policies by changing the proportion of payments made with each credit card. The rate of which households change their behavior follows a logic that is similar to the credit card providers, as outlined in Eq. (5). As a consequence of these interactions, the market share of each credit card providers gradually stabilize over time and the system achieves a Nash equilibrium.

Outputs

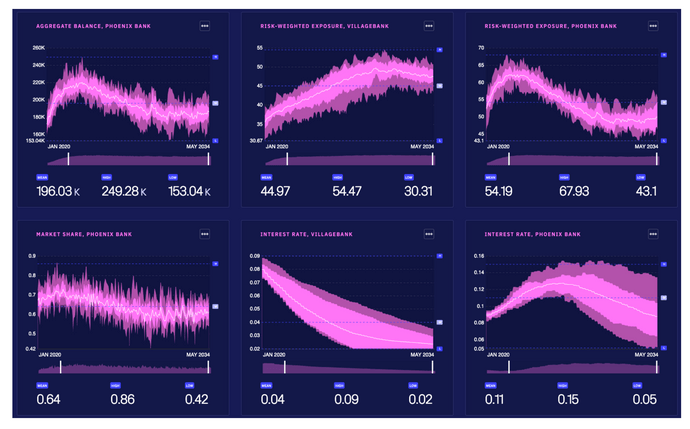
The figure below provides an example of the model in action, and the range of outputs when a Monte Carlo simulation is performed.

The model was initialized with two credit card providers (Phoenix Bank and Villagebank): both of which started with the same interest rate, but Phoenix Bank provided its customers with a rewards program.

As Villagebank does not have a rewards program, it is forced to respond by reducing its interest rates over time to remain competitive. Phoenix Bank, on the other hand, is able to progressively raise its interest rates and maintain its market share, but only up to a certain extent. The system eventually reached a state of equilibrium, in terms of the aggregate balance, risk-weighted exposure and market share.

Future Work

The Simudyne-powered credit card model has successfully demonstrated the practicality of using ABMs in the application of finance. In particular, it showed that: (i) the credit card providers are capable of adapting to each other’s policies to compete for market share; (ii) individual households then respond by altering their spending patterns; and (iii) the system eventually achieved Nash equilibrium.

While this is a novel approach relative to existing methodologies, further work can be done to incorporate additional functionalities into this ABM, such as:

• Adoption of a non-constant interest rate, such as the provision of lower interest rates to households with a better credit score, which can improve the competitiveness and market share of credit card providers.

• Incorporation of additional metrics such as the net interest income (NII) and net interest margin (NIM) to account for cost elements as credit card providers reduce their interest rates and/or increase their reward factors.

• Implementation of a credit loss penalty, where individual households can default when they are not able to cover the minimum repayment. By doing so, an additional strategy can be implemented where credit card providers actively manage their risk by only accepting the right type of customers with a higher credit score.