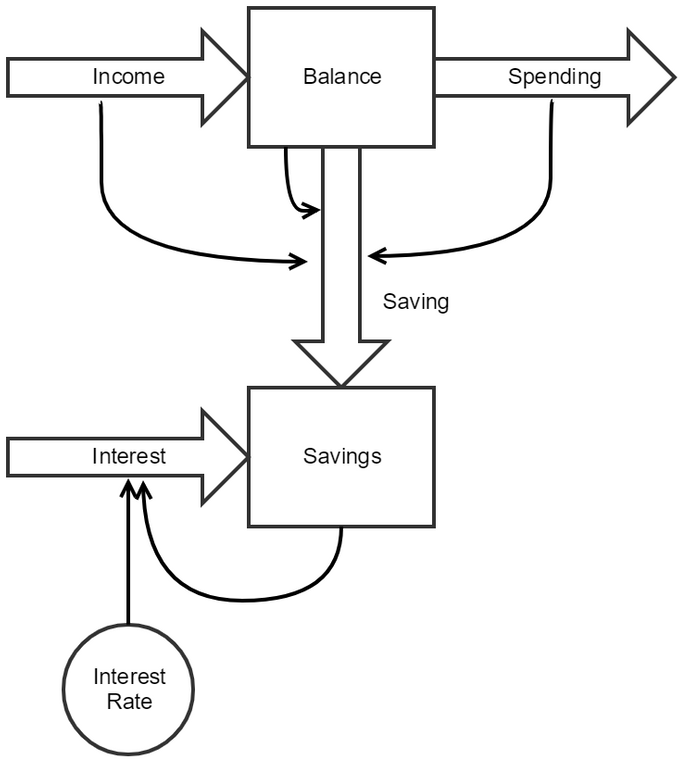
Below is a CLD style diagram representing a Checking & Savings account. We have a balance on our determined by out Income and Spending, and we have a basic plan set up where as long as our balance is above a certain threshold we'll transfer the excess to our Savings to maximize our return on interest.
You'll notice that there are two types of arrows in this design meant to denote the difference between flows and dependencies. This will become clearer as we look into the actual functional requirements for the values of these flows.
Balance = 5000 per month
Spending = 4000 per month
Saving = Min(Balance, Max(500, (Income + Balance - Spending - 2000)))
Interest = Savings * Interest Rate
Given these two simple equations let's begin to compose our model.
@SystemDynamicsSettings(resolution = 1)
public class BankingModel extends SystemDynamicsModel {
}
We've defined our model, we're extending from a SystemDynamicsModel so that our dependencies are built and our stocks are properly calculated. We also define the resolution here, although the default will always be 1.
Now let's add our stocks and the basic flows for Income/Spending
@SystemDynamicsSettings(resolution = 1)
public class BankingModel extends SystemDynamicsModel {
@Stock public double Balance = 0.0;
@Stock public double Savings = 0.0;
@Intermediate public double InterestRate 0.5;
@Flow(to = "Balance")
public double Income() {
return 5000.0;
}
@Flow(from = "Balance")
public double Spending() {
return 4000.0;
}
}
While a typical bank would want you to start with a positive balance, for now, let's simplify and keep it at 0. You'll notice that we've not specified any arguments or a complete source/destination for the two flows.
This is because we've simplified that our income comes from some 'source' be it employer(s), stocks, etc. and has gone out via spending. You should feel empowered to extend this such that spending is divided into fixed and variable costs and potentially use that to inform value of spending changes, and how it affects savings.
And now our finished model as we compose the above equations into flows.
@SystemDynamicsSettings(resolution = 1)
public class BankingModel extends SystemDynamicsModel {
@Stock public double Balance = 0.0;
@Stock public double Savings = 0.0;
@Intermediate public double InterestRate 0.5;
@Flow(to = "Balance")
public double Income() {
return 5000.0;
}
@Flow(from = "Balance")
public double Spending() {
return 4000.0;
}
@Flow(
from = "Balance",
to = "Savings",
args = {"Balance", "Income", "Spending"}
)
public double Saving(double bal, double inc, double spe) {
double adjusted = inc + bal - spe - 2000;
double ret = Math.min(bal, Math.max(500, adjusted));
return ret;
}
@Flow(
to = "Savings",
args = {"Savings", "InterestRate"}
)
public double Interest(double save, double irate) {
return save * irate;
}
}
You'll notice we decided to create a local variable called 'adjusted' in the Saving flow. This is for easier readability and testing. However, let's make a few changes so we'll be able to see and interact with this model in the Console by adding the core annotations for Input & Variable.
@SystemDynamicsSettings(resolution = 1)
public class BankingModel extends SystemDynamicsModel {
@Variable @Stock public double Balance = 0.0;
@Variable @Stock public double Savings = 0.0;
@Input @Intermediate public double InterestRate = 0.5;
@Flow(to = "Balance")
public double Income() {
return 5000.0;
}
@Flow(from = "Balance")
public double Spending() {
return 4000.0;
}
@Flow(
from = "Balance",
to = "Savings",
args = {"Balance", "Income", "Spending"}
)
public double Saving(double bal, double inc, double spe) {
double adjusted = inc + bal - spe - 2000;
double ret = Math.min(bal, Math.max(500, adjusted));
return ret;
}
@Flow(
to = "Savings",
args = {"Savings", "InterestRate"}
)
public double Interest(double save, double irate) {
return save * irate;
}
}
Now when we run our model we'll see that our Balance will add value eventually plateauing at 2000. As well because we've set a very-high interest rate to be calculated every month that our Savings will over time increase dramatically.